Beranda

Science Technology Engineering Math
Struktur Anatomi dan Siklus Hidup Nyamuk

Membuat Perangkap Nyamuk Berfermentasi Gula yang Optimal

Menggunakan Model Matematika Sederhana dengan Pendekatan STEM

🔬 Kimia & Biologi ⚙️ Engineering 📊 Matematika 💹 Ekonomi

4
Disiplin Ilmu
5E
Model Saintifik
CO₂
Atraktan Nyamuk
∞
Ramah Lingkungan

📋 Latar Belakang Masalah

Di Indonesia, ancaman penyakit tular nyamuk seperti Demam Berdarah Dengue (DBD) masih menjadi persoalan kesehatan yang serius. Setiap tahun ribuan kasus dilaporkan, terutama karena nyamuk Aedes aegypti berkembang biak sangat cepat di lingkungan tropis. Tantangan ini menjadi lebih kompleks di Provinsi Papua, yang tidak hanya endemis DBD tetapi juga merupakan episentrum malaria nasional. Penyakit malaria sendiri ditularkan oleh nyamuk Anopheles betina, yang banyak berkembang di wilayah rawa, hutan, dan daerah lembap. Kondisi geografis yang ekstrem, wilayah terpencil, serta keterbatasan akses layanan kesehatan membuat upaya pengendalian nyamuk secara konvensional tidak selalu efektif.

Meskipun DBD dan malaria ditularkan oleh spesies nyamuk berbeda, keduanya memiliki kesamaan dalam mekanisme mencari inang, yaitu sangat bergantung pada deteksi Karbon Dioksida (CO₂) yang dihembuskan manusia. Fakta biologis ini membuka peluang pendekatan inovatif dalam pengendalian nyamuk dengan memanfaatkan CO₂ sebagai umpan.

Fakta Penting:
  • Indonesia termasuk negara endemis DBD tertinggi di Asia Tenggara
  • Papua menghadapi "beban ganda" — endemis DBD sekaligus episentrum malaria nasional
  • Baik nyamuk Aedes aegypti (DBD) maupun Anopheles (malaria) tertarik pada CO₂ yang dihembuskan manusia
  • Penggunaan insektisida kimia berlebihan menimbulkan resistensi dan pencemaran lingkungan
  • Diperlukan metode pengendalian nyamuk yang ramah lingkungan, murah, dan efektif

Mengapa Perangkap Fermentasi?

Proses fermentasi gula oleh ragi (Saccharomyces cerevisiae) menghasilkan CO₂ yang mampu menarik nyamuk secara alami. Karena baik nyamuk DBD maupun malaria sama-sama menggunakan sensor CO₂ untuk menemukan inangnya, perangkap berbasis fermentasi berpotensi efektif untuk kedua jenis nyamuk tersebut.

Rumusan Masalah

  1. Bagaimana komposisi optimal gula dan ragi untuk menghasilkan CO₂ maksimum?
  2. Bagaimana model matematika dapat menjelaskan efektivitas perangkap nyamuk?
  3. Bagaimana kelayakan ekonomi produksi perangkap nyamuk ramah lingkungan?

🎯 Tujuan Pembelajaran

  1. Memahami reaksi fermentasi gula dan hubungannya dengan produksi CO₂
  2. Menganalisis perilaku biologis nyamuk terhadap atraktan CO₂
  3. Menggunakan model matematika untuk menentukan komposisi optimal
  4. Mendesain prototipe perangkap nyamuk dengan pendekatan engineering
  5. Menganalisis potensi ekonomi produk ramah lingkungan

💡 Solusi yang Ditawarkan

Kami mengusulkan perangkap nyamuk berbasis fermentasi gula yang memanfaatkan prinsip-prinsip STEM secara terpadu.

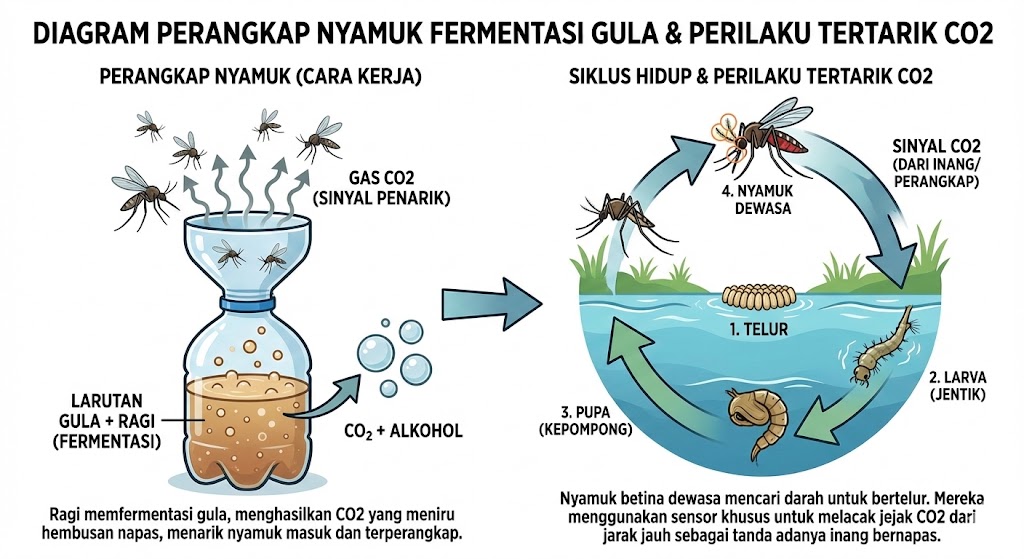
Prinsip Kerja

  1. Fermentasi: Campuran gula + ragi + air hangat menghasilkan CO₂ secara kontinu
  2. Atraksi: CO₂ menarik nyamuk menuju perangkap (meniru pernapasan manusia)
  3. Perangkap: Desain botol terbalik mencegah nyamuk keluar setelah masuk
  4. Optimasi: Model matematika menentukan rasio bahan terbaik

Komponen Alat

BahanJumlahFungsi
Botol plastik bekas 0.6-1.5L1 buahWadah perangkap
Gula pasir... gramSubstrat fermentasi
Ragi roti (yeast)... gramMikroorganisme fermentasi
Air hangat (± ...°C)... mlMedia larutan
Kertas/kain hitamsecukupnyaPenarik visual nyamuk

Desain Perangkap & Perilaku Nyamuk

Diagram Perangkap Nyamuk Fermentasi Gula dan Perilaku Tertarik CO2

Keunggulan Solusi

♻️
Ramah Lingkungan
Rp5K
Biaya Murah
DIY
Mudah Dibuat
24h
Aktif Seharian

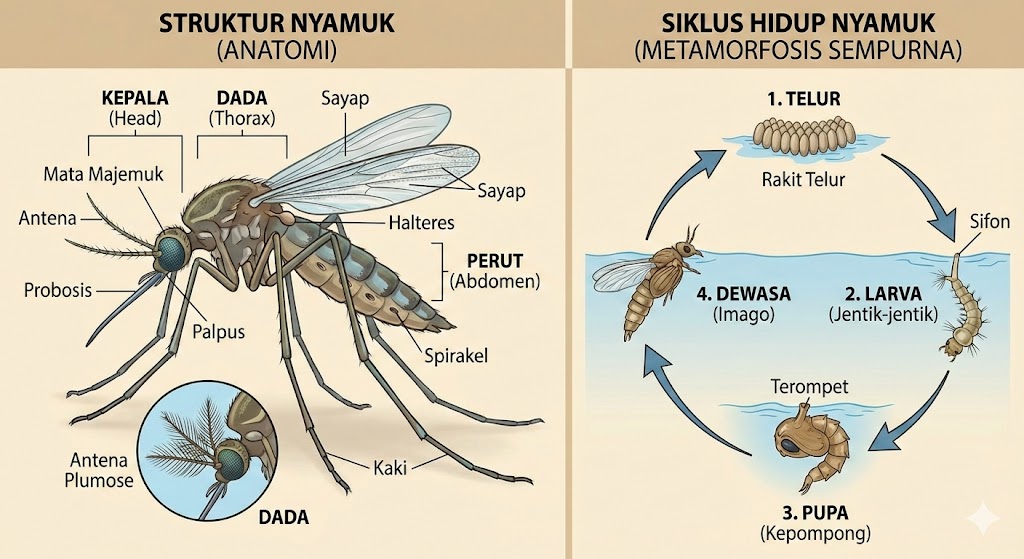
🧬 Biologi: Siklus Hidup & Perilaku Nyamuk

Siklus Hidup Aedes aegypti

🥚
Telur
Diletakkan di dinding wadah air. Tahan kering hingga 1 tahun. ±1-2 hari menetas.
🐛
Larva
Hidup di air, bernapas di permukaan. 4 tahap instar. ±5-10 hari.
🫘
Pupa
Fase istirahat, tidak makan. Berbentuk koma. ±2-3 hari.
🦟
Dewasa
Nyamuk betina menggigit untuk bertelur. Hidup ±2-4 minggu.
Struktur Anatomi Nyamuk dan Siklus Hidup (Metamorfosis Sempurna)

Struktur anatomi nyamuk dan siklus hidup metamorfosis sempurna (Telur → Larva → Pupa → Dewasa)

Perilaku Pencarian Inang

Nyamuk Aedes aegypti menggunakan 3 mekanisme sensorik untuk menemukan inang:

  1. Deteksi CO₂ (jarak jauh: 10-50 meter) — Organ maxillary palp mendeteksi gradien CO₂
  2. Bau tubuh (jarak menengah: 1-10 meter) — Asam laktat, amonia, asam lemak
  3. Panas & visual (jarak dekat: <1 meter) — Radiasi inframerah & warna gelap

Mengapa CO₂ Efektif sebagai senyawa kimia yg mempunyai daya tarik terhadap serangga (Atraktan)?

AspekPenjelasan
JangkauanCO₂ terdeteksi nyamuk hingga radius 50 meter
SpesifisitasNyamuk betina (penggigit) paling sensitif terhadap CO₂
MekanismeReseptor gustatori Gr1, Gr2, Gr3 pada antena nyamuk
ResponsCO₂ memicu perilaku terbang zig-zag mengikuti gradien konsentrasi
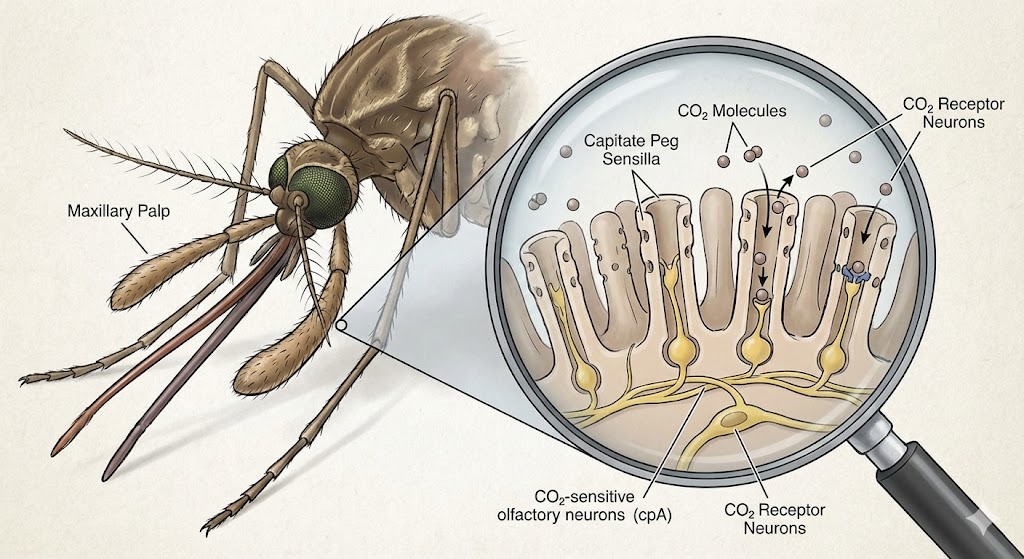
Reseptor CO2 pada Maxillary Palp Nyamuk — Capitate Peg Sensilla dan CO2 Receptor Neurons

Reseptor CO₂ pada maxillary palp nyamuk: molekul CO₂ dideteksi oleh capitate peg sensilla yang mengandung neuron reseptor khusus (cpA)

Perbandingan Karakteristik Nyamuk

Perangkap fermentasi CO₂ menargetkan dua vektor utama penyakit di Indonesia. Berikut perbandingan karakteristik keduanya:

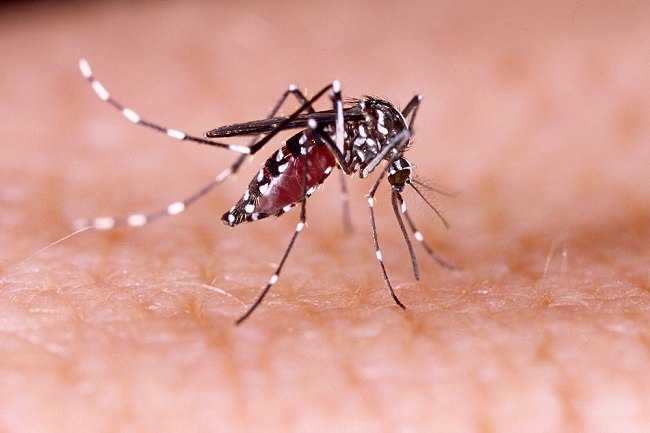
Nyamuk Aedes aegypti

Aedes aegypti — vektor DBD

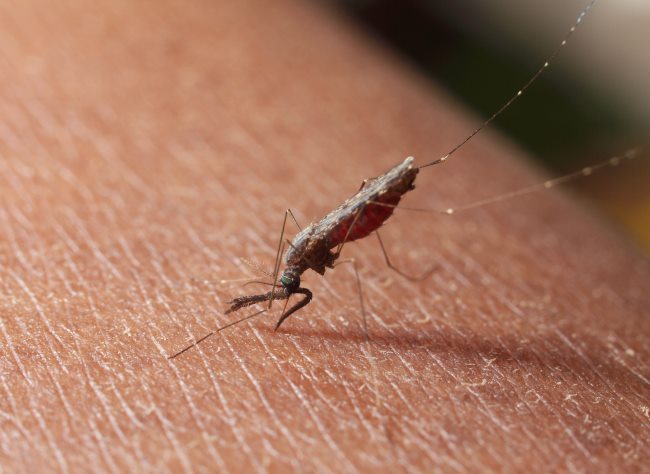
Nyamuk Anopheles

Anopheles — vektor Malaria

Aspek Aedes aegypti Anopheles
Penyakit yang ditularkan DBD, Zika, Chikungunya Malaria
Waktu aktif menggigit Pagi (08.00–10.00) & sore (15.00–17.00) Malam hari (18.00–05.00)
Preferensi cahaya Aktif siang (diurnal) Aktif malam (nokturnal)
Habitat bertelur Air bersih tergenang (bak mandi, drum, vas) Air alami: rawa, sawah, genangan tanah
Lingkungan favorit Perkotaan / pemukiman Pedesaan, hutan, rawa
Jarak terbang ±100 meter Bisa >1 km (tergantung spesies)
Kebutuhan darah Betina butuh protein darah untuk telur Sama: betina butuh darah
Bentuk telur Satu-satu di dinding air Bergerombol di permukaan air
Mengapa perangkap CO₂ efektif untuk keduanya? Meskipun Aedes dan Anopheles berbeda waktu aktif dan habitat, keduanya mengandalkan deteksi CO₂ untuk menemukan inang. Perangkap fermentasi yang menghasilkan CO₂ secara kontinyu dapat bekerja 24 jam — menarik Aedes di siang hari dan Anopheles di malam hari.

⚗️ Kimia: Reaksi Fermentasi

Fermentasi alkohol adalah proses metabolisme anaerobik di mana ragi (Saccharomyces cerevisiae) mengubah glukosa menjadi etanol dan karbon dioksida.

Reaksi Utama

\[\ce{C6H12O6 -> 2C2H5OH + 2CO2} + \text{Energi}\]
Glukosa → Etanol + Karbon Dioksida + Energi (ATP)
Gas CO₂ inilah yang dimanfaatkan untuk menarik nyamuk pada perangkap. Nyamuk mendeteksi CO₂ dari jarak jauh, sehingga fermentasi gula menjadi "umpan" yang meniru napas manusia.

Jika Menggunakan Gula Pasir (Sukrosa)

Gula dapur = sukrosa (\(\ce{C12H22O11}\)) tidak langsung difermentasi. Ragi akan memecahnya dulu menjadi glukosa + fruktosa.

Tahap 1 — Hidrolisis Sukrosa
\[\ce{C12H22O11 + H2O -> 2 C6H12O6}\]
(Sukrosa → Glukosa + Fruktosa)
Tahap 2 — Fermentasi

Masing-masing gula sederhana difermentasi:

\[\ce{C6H12O6 -> 2C2H5OH + 2CO2}\]

Karena ada 2 molekul gula sederhana dari setiap molekul sukrosa, total CO₂ yang dihasilkan lebih banyak.

Stoikiometri: Dari Gula Pasir hingga CO₂

Bahan awal perangkap kita: 50 gram gula pasir (sukrosa, \(\ce{C12H22O11}\), \(M_r = 342\)).

Gula pasir bukan glukosa murni — ragi harus memecahnya dulu. Mari telusuri perjalanan dari gula pasir hingga menjadi CO₂ langkah demi langkah.

Langkah 1 — Hitung mol sukrosa (gula pasir):
\[n_{\text{sukrosa}} = \frac{\text{massa}}{M_r} = \frac{50}{342} = 0{,}146 \text{ mol}\]
Langkah 2 — Hidrolisis: sukrosa → glukosa

Setiap 1 mol sukrosa dipecah menjadi 2 mol gula sederhana (glukosa + fruktosa, keduanya \(M_r = 180\)):

\[\ce{C12H22O11 + H2O -> 2 C6H12O6}\]
\[n_{\text{glukosa}} = 2 \times 0{,}146 = 0{,}292 \text{ mol}\]
Setara dengan \(0{,}292 \times 180 = 52{,}6\) gram glukosa murni
Langkah 3 — Fermentasi: glukosa → etanol + CO₂

Setiap 1 mol glukosa menghasilkan 2 mol CO₂:

\[\ce{C6H12O6 -> 2C2H5OH + 2CO2}\]
\[n_{\ce{CO2}} = 2 \times 0{,}292 = 0{,}584 \text{ mol}\]
Langkah 4 — Hitung volume CO₂:
\[V_{\ce{CO2}} = n \times 22{,}4 = 0{,}584 \times 22{,}4 = 13{,}08 \text{ liter (STP)}\]

Ringkasan Stoikiometri (dari 50g Gula Pasir)

TahapZat\(M_r\)MolMassa / Volume
AwalSukrosa (\(\ce{C12H22O11}\))3420,14650 gram
HidrolisisGlukosa (\(\ce{C6H12O6}\))1800,29252,6 gram
FermentasiEtanol (\(\ce{C2H5OH}\))460,58426,9 gram
Fermentasi\(\ce{CO2}\)440,58413,08 L (STP)
Perbandingan cepat: 1 mol sukrosa menghasilkan 4 mol CO₂ (bukan 2), karena 1 sukrosa dipecah menjadi 2 glukosa, masing-masing menghasilkan 2 CO₂. Jadi gula pasir sebenarnya sedikit lebih efisien per gram dibanding glukosa murni (13,08 L vs 12,44 L dari 50g).
Seberapa banyak 13 liter CO₂?
Setara dengan ± 9 botol air mineral 1,5L atau sekitar 1 balon besar yang ditiup penuh. Volume sebesar ini cukup untuk menarik nyamuk dalam radius beberapa meter selama berjam-jam.

Mengapa Reaksi Ini Terjadi Secara Alami?

Konsep Entropi (Ketidakteraturan):

Pada fermentasi, zat cair (larutan glukosa) berubah menjadi gas (CO₂). Gas memiliki molekul yang lebih tersebar dan tidak teratur dibanding cairan. Dalam kimia, peningkatan ketidakteraturan ini disebut peningkatan entropi.

Reaksi yang meningkatkan entropi cenderung terjadi secara spontan — artinya reaksi berjalan sendiri tanpa perlu energi tambahan terus-menerus.

Analogi: Bayangkan balon yang ditiup — molekul gas di dalam balon menyebar ke segala arah secara acak. Sama seperti itu, CO₂ yang dihasilkan fermentasi menyebar keluar larutan dan menarik nyamuk dari berbagai arah.

Faktor yang Mempengaruhi Laju Fermentasi

  1. Suhu: Optimal 30-35°C (enzim zimase aktif)
  2. Konsentrasi gula: Terlalu tinggi → plasmolisis sel ragi
  3. pH: Optimal pH 4-5 (sedikit asam)
  4. Rasio ragi/gula: Mempengaruhi kecepatan konversi
FaktorJika Terlalu TinggiDampak pada Perangkap
Suhu> 40°CRagi mati, produksi CO₂ berhenti
Konsentrasi Gula> 25%Osmosis/plasmolisis — sel ragi rusak
Jumlah RagiBerlebihanSubstrat (gula) cepat habis, perangkap tidak tahan lama

📐 Matematika: Model Optimasi

1. Model Eksponensial: Dari Reaksi Kimia ke Matematika

Dari pengamatan ke model:

Fermentasi terjadi karena ragi mengonsumsi gula sebagai sumber energi. Semakin banyak gula tersedia, semakin cepat proses fermentasi berlangsung. Sebaliknya, ketika gula berkurang, laju fermentasi juga menurun.

Analogi: Seperti bensin di motor — tangki penuh, mesin bisa bekerja kencang. Tangki hampir kosong, mesin melambat. Gula = bensin, ragi = mesin.

Jika kita mengamati fermentasi secara eksperimen, polanya selalu sama: di awal gelembung CO₂ banyak dan cepat, lalu makin lama makin jarang. Ini karena gula yang tersedia terus berkurang. Artinya, laju berkurangnya gula sebanding dengan jumlah gula yang masih tersisa.

Langkah 1 — Dari Observasi ke Persamaan Diferensial

Tahap 1 — Pernyataan proporsional:
\[\text{Laju konsumsi gula} \;\propto\; S\]
"Makin banyak gula tersisa, makin cepat gula dikonsumsi"
Tahap 2 — Ubah menjadi persamaan:

Hubungan proporsional diubah menjadi persamaan dengan konstanta \(k\):

\[\text{Laju} = k \cdot S\]

Karena gula berkurang (bukan bertambah), kita beri tanda negatif:

\[\frac{dS}{dt} = -kS\]
Kinetika orde pertama — laju perubahan gula terhadap waktu

Variabel yang Digunakan

SimbolArtiSatuan
\(S(t)\)Jumlah gula pada waktu \(t\)gram atau mol
\(S_0\)Jumlah gula awal (saat \(t = 0\))gram atau mol
\(\dfrac{dS}{dt}\)Laju perubahan gula — "seberapa cepat gula berkurang tiap jam"gram/jam atau mol/jam
\(k\)Konstanta laju fermentasi1/jam
\(t\)Waktu fermentasijam
Tanda \(-\)Menunjukkan gula berkurang, bukan bertambah
Apa arti konstanta \(k\)?
Nilai \(k\) menentukan seberapa cepat fermentasi berlangsung. Nilainya dipengaruhi oleh jumlah ragi, suhu, dan pH.
  • \(k\) besar → fermentasi cepat (gula cepat habis, CO₂ deras di awal)
  • \(k\) kecil → fermentasi lambat (gula habis perlahan, CO₂ stabil lebih lama)

Langkah 2 — Penyelesaian Persamaan Diferensial

Bayangan sebelum hitung: Bayangkan kamu memakan setengah dari sisa kue setiap jam. Jam pertama kamu makan 50%, jam kedua 25% (setengah dari sisa), jam ketiga 12,5%, dan seterusnya. Gula tidak turun lurus — melainkan melengkung. Pola inilah yang kita cari solusinya.
Langkah 2a — Pisahkan variabel:
\[\frac{1}{S}\,dS = -k\,dt\]
Langkah 2b — Integralkan kedua ruas:
\[\int \frac{1}{S}\,dS = \int -k\,dt\]
Hasil: \(\ln|S| = -kt + C\)
Langkah 2c — Eksponensialkan:
\[S = e^{-kt+C} = C_1 \cdot e^{-kt}\]
Langkah 2d — Gunakan kondisi awal (saat \(t = 0\), \(S = S_0\)):
\[S_0 = C_1 \cdot e^{0} \quad \Rightarrow \quad C_1 = S_0\]
\[\boxed{S(t) = S_0 \cdot e^{-kt}}\]
Model peluruhan eksponensial — gula berkurang secara eksponensial seiring waktu

Langkah 3 — Dari Gula Terpakai ke CO₂

Gula yang sudah terfermentasi pada waktu t:

\[S_{\text{pakai}}(t) = S_0 - S(t) = S_0 - S_0 e^{-kt} = S_0\!\left(1 - e^{-kt}\right)\]

Dari stoikiometri reaksi: 1 mol glukosa menghasilkan 2 mol CO₂. Maka:

\[\boxed{\ce{CO2}(t) = 2S_0\!\left(1 - e^{-kt}\right)}\]
Total CO₂ yang dihasilkan bertambah seiring waktu (akumulasi dari gula yang terpakai)

Langkah 4 — CO₂ Maksimum

Ketika waktu sangat lama (t → ∞), semua gula habis terfermentasi:

\[e^{-kt} \to 0 \quad \text{sehingga} \quad \ce{CO2}_{\text{maks}} = 2S_0\]
Sesuai dengan stoikiometri total reaksi: seluruh glukosa → 2× mol CO₂

Langkah 5 — Laju Produksi CO₂

Seberapa cepat CO₂ dihasilkan pada waktu tertentu? Turunkan \(\ce{CO2}(t)\) terhadap waktu:

Turunan:
\[r_{\ce{CO2}}(t) = \frac{d[\ce{CO2}]}{dt} = 2S_0 \cdot \frac{d}{dt}\!\left(1 - e^{-kt}\right)\]
\[r_{\ce{CO2}}(t) = 2S_0 \cdot k e^{-kt}\]
\[\boxed{r_{\ce{CO2}}(t) = 2kS_0 \cdot e^{-kt}}\]
Laju produksi CO₂ tertinggi di awal, lalu menurun eksponensial

Karena \(S(t) = S_0 e^{-kt}\), maka:

\[\boxed{r_{\ce{CO2}}(t) = 2k \cdot S(t)}\]
Laju CO₂ selalu sebanding dengan gula yang tersisa — semakin sedikit gula, semakin lambat CO₂ dihasilkan

Alur Ringkas: Kimia → Matematika

  1. Reaksi kimia: \(\ce{C6H12O6 -> 2CO2 + 2C2H5OH}\)
  2. Stoikiometri: 1 mol glukosa → 2 mol CO₂
  3. Model laju: \(\frac{dS}{dt} = -kS\)
  4. Solusi eksponensial: \(S(t) = S_0 e^{-kt}\)
  5. CO₂ akumulasi: \(\ce{CO2}(t) = 2S_0(1 - e^{-kt})\)
  6. Laju CO₂: \(r_{\ce{CO2}}(t) = 2kS_0 e^{-kt}\)

Simulasi Interaktif: Visualisasi \(S(t)\) dan \(\ce{CO2}(t)\)

Gerakkan slider untuk melihat bagaimana nilai \(S_0\) (gula awal) dan \(k\) (konstanta laju) mempengaruhi bentuk kurva.

10g50 g100g
—
0,050,201,00
Pembacaan grafik:
  • Gula tinggal setengah pada: —
  • CO₂ maksimum: —
  • Laju CO₂ awal: —
Coba sendiri:
  • Geser \(k\) ke kanan (besar) — perhatikan gula habis lebih cepat, tapi CO₂ juga cepat berhenti naik
  • Geser \(k\) ke kiri (kecil) — gula habis perlahan, CO₂ naik lebih lambat tapi lebih lama
  • Tambah \(S_0\) — total CO₂ akhir meningkat (garis biru naik lebih tinggi)
Makna untuk Proyek Perangkap Nyamuk:
  • Gula (\(S_0\)) menentukan total CO₂ yang bisa dihasilkan — makin banyak gula, makin banyak CO₂
  • Ragi mempengaruhi nilai \(k\) (kecepatan reaksi) — makin banyak ragi, makin cepat CO₂ keluar, tapi gula juga lebih cepat habis
  • Model eksponensial memprediksi berapa lama larutan perangkap masih efektif menghasilkan CO₂
  • Dengan mengatur \(S_0\) dan \(k\), kita bisa mengoptimalkan agar perangkap menghasilkan CO₂ yang cukup selama waktu yang diinginkan
Dasar teori: Model peluruhan eksponensial (\(dS/dt = -kS\)) merupakan kinetika reaksi orde pertama yang umum digunakan dalam kimia dan biokimia. Seluruh turunan di atas mengikuti kaidah kalkulus standar (separasi variabel & integrasi). Nilai konstanta laju \(k\) dalam simulator ini bersifat ilustratif untuk tujuan pembelajaran — pada praktiknya, nilai \(k\) perlu ditentukan melalui eksperimen.

2. Fungsi Efektivitas Gaussian

Model eksponensial di atas menunjukkan berapa banyak CO₂ yang dihasilkan dari gula. Tapi apakah semua CO₂ itu efektif menarik nyamuk? Tidak — efektivitasnya bergantung pada kondisi: suhu, rasio ragi, dan konsentrasi larutan.

Setiap faktor memiliki titik optimal. Terlalu rendah atau terlalu tinggi, efektivitas menurun. Pola ini membentuk kurva lonceng (Gaussian):

Analogi: Seperti volume musik — terlalu pelan tidak terdengar, terlalu keras tidak nyaman. Ada titik "pas" di tengah yang paling enak didengar. Begitu pula komposisi perangkap nyamuk!
\[E = f(T) \times f(R) \times f(C) \times 100\%\]
\[f(T) = e^{-\frac{1}{2}\left(\frac{T-32}{5}\right)^2} \qquad f(R) = e^{-\frac{1}{2}\left(\frac{R-10}{4}\right)^2} \qquad f(C) = e^{-\frac{1}{2}\left(\frac{C-20}{8}\right)^2}\]
\(T\) = suhu (°C), \(R\) = rasio ragi/gula (%), \(C\) = konsentrasi larutan (%)
Nilai Optimal:
  • Suhu: 32°C (puncak aktivitas enzim zimase)
  • Rasio ragi/gula: 10% (keseimbangan substrat-enzim)
  • Konsentrasi larutan: 20% (cukup substrat tanpa plasmolisis)
Dasar teori: Konsep bahwa aktivitas enzim memiliki titik optimum dan menurun di kedua sisi merupakan prinsip biokimia yang mapan. Bentuk kurva Gaussian (distribusi normal) digunakan sebagai pendekatan. Nilai optimal (suhu 32°C, rasio 10%, konsentrasi 20%) didasarkan pada literatur umum fermentasi ragi, namun parameter lebar kurva (σ) bersifat ilustratif.

3. Model Produksi CO₂ Sepanjang Waktu

Model eksponensial (bagian 1) menghitung total CO₂, sementara Gaussian (bagian 2) menentukan efektivitas kondisi. Sekarang kita gabungkan keduanya dengan memperhitungkan faktor waktu — karena produksi CO₂ per jam tidak konstan. Ada 3 fase yang terjadi secara alami:

\[P(t) = v \cdot L(t) \cdot D(t)\]
\(L(t) = \frac{1}{1+e^{-0{,}5(t-2)}}\) [fase lag]   |   \(D(t) = e^{-0{,}03 \cdot \max(0,\, t-12)}\) [fase penurunan]
Tiga Fase Produksi CO₂:
  1. Fase Adaptasi (0–4 jam): Ragi "bangun" dan mulai bekerja — produksi CO₂ masih rendah
  2. Fase Puncak (4–12 jam): Ragi aktif penuh, gula masih banyak — CO₂ maksimal
  3. Fase Penurunan (>12 jam): Gula mulai habis — produksi melambat
Dasar teori: Model ini menggabungkan tiga komponen yang masing-masing mapan secara teori: laju awal v menggunakan kinetika Michaelis-Menten (model standar enzimologi), fase lag L(t) menggunakan fungsi sigmoid/logistik (umum dalam model pertumbuhan mikroba), dan fase penurunan D(t) menggunakan peluruhan eksponensial. Penggabungan ketiganya (P = v × L × D) merupakan pendekatan komposit untuk ilustrasi — parameter waktu (fase lag 2 jam, penurunan mulai 12 jam) bersifat estimasi dan dapat berbeda pada kondisi eksperimen sesungguhnya.

📐 4. Optimasi Matematis: Mencari Komposisi Terbaik

Bagian 1–3 di atas adalah model deskriptif — menjelaskan bagaimana fermentasi bekerja. Sekarang kita gunakan model tersebut untuk benar-benar mencari komposisi terbaik secara matematis.

Mendefinisikan Fungsi Tujuan

Pertanyaan optimasi: Berapa komposisi gula, ragi, suhu, dan air agar perangkap menghasilkan CO₂ efektif yang maksimal?

Total CO₂ efektif sebanding dengan volume CO₂ (dari stoikiometri) dikalikan efektivitas kondisi:

\[J = V_{\ce{CO2}}(g) \times E(T, R, C)\]
\(J\) = fungsi tujuan yang ingin dimaksimalkan

Dengan:

  • \(V_{\ce{CO2}}(g) = \frac{g}{180} \times 2 \times 22{,}4\) liter — volume CO₂ dari stoikiometri, bergantung pada jumlah gula \(g\)
  • \(E = f(T) \times f(R) \times f(C)\) — efektivitas, bergantung pada suhu, rasio ragi, dan konsentrasi

A. Optimasi Suhu (\(dE/dT = 0\))

Karena \(V_{\ce{CO2}}\) tidak bergantung pada suhu, kita cukup memaksimalkan \(f(T)\):

\[f(T) = e^{-\frac{1}{2}\left(\frac{T-32}{5}\right)^2}\]
Turunan pertama:
\[\frac{df}{dT} = f(T) \cdot \left(-\frac{T-32}{25}\right) = 0\]

Karena \(f(T) > 0\) selalu, maka syaratnya:

\[T - 32 = 0 \quad \Rightarrow \quad T^* = 32°\text{C}\]
Uji turunan kedua (konfirmasi maksimum):
\[\left.\frac{d^2f}{dT^2}\right|_{T=32} = f(32) \cdot \left(-\frac{1}{25}\right) = -\frac{1}{25} < 0 \quad \Rightarrow \quad \text{Terbukti maksimum}\]
Dengan cara yang sama, \(f(R)\) maksimum saat \(R^* = 10\%\) dan \(f(C)\) maksimum saat \(C^* = 20\%\). Masing-masing bisa dibuktikan dengan turunan pertama = 0 dan turunan kedua < 0.

B. Optimasi Jumlah Gula — Trade-off Nyata

Di sinilah optimasi menjadi menarik. Jumlah gula (g) mempengaruhi dua hal sekaligus:

  • Lebih banyak gula → lebih banyak CO₂ (\(V_{\ce{CO2}}\) naik) — ini bagus
  • Tapi konsentrasi C naik → \(f(C)\) turun jika \(C > 20\%\) — ini buruk

Ada titik keseimbangan di mana tambahan gula sudah tidak sebanding dengan penurunan efektivitas. Titik inilah yang kita cari!

Untuk air tetap (w ml), fungsi tujuan terhadap gula:

\[J(g) = g \cdot f_C(g) \quad \text{dengan} \quad C(g) = \frac{100g}{w + g}\]
Konstanta stoikiometri dihilangkan karena tidak mempengaruhi lokasi optimum
Turunan pertama (aturan rantai):
\[\frac{dJ}{dg} = f_C + g \cdot f_C \cdot \left(-\frac{C - 20}{64}\right) \cdot \frac{dC}{dg} = 0\]

Dengan \(\frac{dC}{dg} = \frac{100w}{(w + g)^2}\). Bagi kedua ruas dengan \(f_C > 0\):

\[1 = g \cdot \frac{C - 20}{64} \cdot \frac{100w}{(w + g)^2}\]
Persamaan ini tidak bisa diselesaikan secara aljabar sederhana — kita selesaikan secara numerik

Penyelesaian Numerik (w = 200 ml)

Kita hitung J(g) untuk berbagai takaran gula:

Gula (g)C (%)\(f_C\)\(J = g \cdot f_C\)Keterangan
3013.00.68520.6Gula terlalu sedikit
4016.70.91736.7
5020.01.00050.0\(f_C\) maksimum, tapi bukan \(J\) maksimum
5521.60.98154.0
6223.60.90055.8\(J\) maksimum
7025.90.76053.2
8028.60.56345.1
10033.30.24924.9Konsentrasi terlalu tinggi
Hasil optimasi:

Gula optimal \(g^* \approx 62\) gram (bukan 50 gram!). Pada titik ini, konsentrasi \(C = 23{,}6\%\) — sedikit di atas titik optimal \(f_C\) (20%), karena keuntungan dari lebih banyak CO₂ masih lebih besar dari penurunan efektivitas.

Ini menunjukkan bahwa titik optimal keseluruhan berbeda dari titik optimal masing-masing faktor — itulah inti dari optimasi multivariabel.

C. Optimasi Ragi

Untuk rasio ragi/gula optimal R* = 10%, dengan g* = 62 gram:

\[R^* = \frac{100 \times r}{g} = 10\% \quad \Rightarrow \quad r^* = \frac{g^*}{10} = \frac{62}{10} = 6{,}2 \text{ gram}\]

D. Resep Optimal Perangkap Nyamuk

ParameterNilai OptimalMetode
Suhu32°C\(dE/dT = 0\), \(d^2E/dT^2 < 0\)
Gula62 gram\(dJ/dg = 0\) (numerik)
Ragi6,2 gram\(R^* = 10\% \times g^*\)
Air200 mlParameter tetap
Konsentrasi23,6%Hasil dari \(g^*\) dan \(w\)
Mengapa 62g, bukan 50g? Pada 50g gula, konsentrasi tepat 20% (optimal untuk \(f_C\)), tapi total CO₂ masih bisa ditingkatkan. Menambah gula ke 62g menurunkan \(f_C\) sedikit (dari 1,0 ke 0,9), tapi menambah volume CO₂ 24% (dari 50 ke 62 unit). Keuntungan bersih: +11,6%. Di atas 62g, penurunan \(f_C\) sudah lebih besar dari tambahan CO₂.
Catatan: Optimasi di atas mengasumsikan air tetap 200 ml. Jika air juga divariasikan, muncul optimasi dua variabel \((g, w)\) yang lebih kompleks. Siswa dapat mengeksplorasi ini menggunakan grafik interaktif di bawah — coba ubah slider air dan perhatikan bagaimana puncak efektivitas bergeser.

📊 Grafik Interaktif: Pengaruh Komposisi

Saatnya menguji semua model di atas secara visual! Gerakkan slider untuk melihat bagaimana perubahan komposisi mempengaruhi efektivitas \(E\), fungsi tujuan \(J\), dan kurva produksi CO₂.

10g62g150g
1g6.2g20g
20°C32°C45°C
100ml200ml500ml
—
\(f(T)\) Suhu
—
\(f(R)\) Rasio
—
\(f(C)\) Konsentrasi
—
\(E = f(T) \times f(R) \times f(C)\)
—
\(J = V_{\ce{CO2}} \times E\)

Kurva Produksi CO₂ Efektif (24 Jam)

Produksi CO₂ per jam = \(J \times L(t) \times D(t)\), menggabungkan efektivitas Gaussian dengan model waktu (fase lag + penurunan).

Catatan: Grafik di atas menggunakan parameter ilustratif untuk tujuan pembelajaran. Pola umum kurva (bentuk lonceng pada efektivitas, fase lag–puncak–penurunan pada produksi CO₂) sesuai dengan teori, namun nilai numerik spesifik dapat berbeda dari hasil eksperimen nyata. Siswa dianjurkan membandingkan pola grafik ini dengan data eksperimen mereka sendiri pada bagian Proses 5E.
Referensi teori:
  • Kinetika Michaelis-Menten — L. Michaelis & M. Menten (1913), model standar laju reaksi enzimatis
  • Distribusi Gaussian — C.F. Gauss, digunakan untuk memodelkan respons biologis terhadap variabel lingkungan
  • Peluruhan eksponensial (orde pertama) — prinsip dasar kinetika kimia untuk reaksi yang lajunya sebanding dengan konsentrasi reaktan
  • Model pertumbuhan logistik — P.F. Verhulst (1838), digunakan untuk fase lag pertumbuhan mikroorganisme

💰 Ekonomi: Potensi Usaha Perangkap Nyamuk Ramah Lingkungan

Analisis Biaya Produksi

KomponenBiaya/UnitKeterangan
Bahan baku (gula, ragi)Rp 2.000Gula 50g + Ragi 5g
Botol bekas + pelapisRp 1.000Daur ulang
Kemasan & labelRp 2.000Branding produk
Tenaga kerjaRp 3.000Perakitan
OverheadRp 2.000Transport, listrik
Total HPPRp 10.000

Simulator Ekonomi

10100500
15rbRp 25.00050rb
-
Pendapatan
-
Laba Bersih
-
Margin (%)
-
BEP (unit)

Proyeksi Pendapatan 12 Bulan

Potensi Pasar:
  • Target: rumah tangga, sekolah, puskesmas, desa wisata
  • Keunggulan kompetitif: ramah lingkungan, tanpa bahan kimia berbahaya
  • Bisa dikembangkan sebagai program kewirausahaan siswa
  • Potensi ekspor ke daerah endemis malaria & DBD

🔬 Proses Saintifik & Enjinering (Model 5E)

1
Eksitasi
2
Eksplorasi
3
Eksperimen
4
Eksplanasi
5
Elaborasi
6
Evaluasi

1. Eksitasi (Engagement)

Tujuan: Membangkitkan rasa ingin tahu dan motivasi belajar siswa.

Aktivitas:

  • Pertanyaan Pemantik: "Mengapa nyamuk selalu menemukan kita meski dalam gelap?"
  • Video Stimulus: Tayangan tentang dampak DBD di Indonesia dan cara nyamuk mendeteksi manusia
  • Diskusi: Siswa berbagi pengalaman tentang cara pengendalian nyamuk di rumah masing-masing
  • Demonstrasi: Guru menunjukkan botol berisi larutan gula+ragi yang menghasilkan gelembung CO₂

Pertanyaan Pengarah:

  1. Apa yang membuat nyamuk tertarik mendekati manusia?
  2. Gas apa yang kita keluarkan saat bernapas?
  3. Bisakah kita "meniru" napas manusia untuk menjebak nyamuk?

2. Eksplorasi (Exploration)

Tujuan: Siswa mengumpulkan informasi dan membangun pemahaman konsep dasar.

Aktivitas:

  • Studi Literatur: Siswa membaca materi tentang fermentasi, siklus hidup nyamuk, dan reaksi kimia
  • Investigasi Kelompok:
    • Kelompok A: Mempelajari reaksi fermentasi & stoikiometri
    • Kelompok B: Mempelajari biologi & perilaku nyamuk
    • Kelompok C: Mempelajari model matematika optimasi
    • Kelompok D: Melakukan survei harga bahan & potensi pasar
  • Penggunaan Simulator: Siswa mencoba simulator interaktif untuk memahami pengaruh variabel

3. Eksperimen (Experiment)

Tujuan: Siswa melakukan percobaan untuk menguji hipotesis dan mengumpulkan data.

Prosedur Eksperimen:

VariabelPerlakuan 1Perlakuan 2Perlakuan 3Kontrol
Gula (g)25501000
Ragi (g)5555
Air (ml)200200200200

Langkah Percobaan:

  1. Potong botol plastik 1.5L menjadi 2 bagian (⅓ atas, ⅔ bawah)
  2. Larutkan gula dalam air hangat (±35°C) di bagian bawah botol
  3. Tambahkan ragi, aduk perlahan
  4. Balik bagian atas botol sebagai corong, masukkan ke bagian bawah
  5. Lapisi sisi luar dengan kertas/kain hitam
  6. Letakkan perangkap di lokasi uji selama 24 jam
  7. Hitung jumlah nyamuk yang terperangkap
  8. Catat data pada tabel pengamatan

Lembar Pengamatan:

Jam ke-Gelembung CO₂Nyamuk TertangkapSuhu LarutanCatatan
0----
2
6
12
24

4. Eksplanasi (Explanation)

Tujuan: Siswa menganalisis data, menjelaskan hasil, dan menghubungkan dengan teori.

Kegiatan Analisis:

  • Analisis Data: Siswa membuat grafik dari data eksperimen menggunakan simulator
  • Diskusi Kelas:
    1. Komposisi mana yang menghasilkan CO₂ paling banyak?
    2. Apakah hasil eksperimen sesuai dengan prediksi model matematika?
    3. Mengapa komposisi tertentu lebih efektif?
    4. Bagaimana hubungan stoikiometri dengan hasil nyata?
  • Koneksi STEM: Siswa menjelaskan bagaimana setiap disiplin ilmu berperan:
    • Kimia → Reaksi fermentasi & stoikiometri
    • Biologi → Perilaku nyamuk terhadap CO₂
    • Matematika → Model optimasi & prediksi
    • Ekonomi → Kelayakan produksi massal

Pertanyaan Refleksi:

  1. Jelaskan mengapa suhu mempengaruhi laju fermentasi!
  2. Hitung mol CO₂ dari eksperimenmu dan bandingkan dengan teori!
  3. Mengapa perubahan dari cairan ke gas (peningkatan entropi) membuat reaksi fermentasi berlangsung spontan?

5. Elaborasi (Elaboration)

Tujuan: Siswa mengembangkan dan menerapkan pengetahuan ke konteks baru.

Proyek Pengembangan:

  • Desain Iterasi: Perbaiki desain perangkap berdasarkan data eksperimen
    • Optimasi komposisi bahan berdasarkan model matematika
    • Modifikasi bentuk perangkap untuk efektivitas maksimal
    • Penambahan atraktan visual (warna hitam, LED UV)
  • Business Plan: Siswa menyusun rencana bisnis sederhana
    • Analisis SWOT produk
    • Strategi pemasaran ramah lingkungan
    • Perhitungan BEP dan proyeksi keuntungan
  • Presentasi: Setiap kelompok mempresentasikan perangkap terbaiknya

Tantangan Engineering:

🏗️
Desain paling menarik nyamuk
📊
Model matematika paling akurat
💡
Inovasi paling kreatif

6. Evaluasi (Evaluation)

Tujuan: Mengukur pemahaman siswa dan refleksi proses pembelajaran.

A. Rubrik Penilaian Proyek

AspekBobotIndikator
Pemahaman Konsep STEM25%Mampu menjelaskan keterkaitan 4 disiplin ilmu
Keterampilan Eksperimen25%Prosedur benar, data akurat, analisis tepat
Model Matematika20%Mampu menggunakan rumus dan menginterpretasi grafik
Desain Engineering15%Perangkap fungsional, efektif, estetis
Analisis Ekonomi15%Perhitungan HPP, BEP, dan proyeksi realistis

B. Soal Evaluasi

1. Reaksi fermentasi glukosa menghasilkan...




2. Nyamuk mendeteksi CO₂ menggunakan organ...




3. Jika ΔS > 0 pada reaksi fermentasi, ini berarti...




4. Dari 50g glukosa (Mr=180), mol CO₂ yang dihasilkan adalah...




5. Jika HPP = Rp10.000 dan harga jual Rp25.000, berapa margin keuntungan?





C. Refleksi Diri

  • Apa yang paling menarik dari proyek ini?
  • Kesulitan apa yang kamu hadapi dan bagaimana mengatasinya?
  • Bagaimana kamu bisa menerapkan prinsip STEM dalam kehidupan sehari-hari?

🧪 Simulator Perangkap Nyamuk Fermentasi

Atur parameter di bawah untuk mensimulasikan efektivitas perangkap nyamuk.

10g62g150g
1g6.2g20g
20°C32°C45°C
100ml200ml500ml
-
Efektivitas (%)
-
Volume CO₂ (ml)
-
Laju CO₂ (ml/jam)
-
Est. Nyamuk/Hari
-
Skor Suhu
-
Skor Rasio
-
Skor Konsentrasi

Kurva Produksi CO₂ (24 Jam)

Peluruhan Substrat vs Akumulasi CO₂

Grafik ini menunjukkan bagaimana gula berkurang (peluruhan eksponensial) sementara total CO₂ bertambah seiring waktu.

📝 Penutup

Kesimpulan

  1. Perangkap nyamuk berbasis fermentasi gula merupakan solusi ramah lingkungan yang efektif memanfaatkan produksi CO₂ dari reaksi fermentasi glukosa oleh ragi.
  2. Model matematika (fungsi Gaussian dan kinetika Michaelis-Menten) dapat digunakan untuk menentukan komposisi optimal: gula 50g, ragi 5g, air 200ml pada suhu 30-35°C.
  3. Pendekatan STEM memungkinkan siswa memahami keterkaitan Kimia (reaksi fermentasi, entropi), Biologi (perilaku nyamuk), Matematika (model eksponensial & optimasi Gaussian), dan Ekonomi (analisis kelayakan usaha).
  4. Proses 5E memfasilitasi pembelajaran yang aktif, kolaboratif, dan bermakna melalui pengalaman langsung.

Manfaat Pembelajaran

AspekKompetensi yang Dicapai
KognitifPemahaman konsep fermentasi, stoikiometri, entropi, model matematika eksponensial
PsikomotorikKeterampilan eksperimen, desain engineering, penggunaan simulator
AfektifKepedulian lingkungan, kolaborasi, berpikir kritis dan kreatif
LiterasiLiterasi sains, numerasi, digital, dan finansial

Saran Pengembangan

  • Uji coba perangkap di berbagai kondisi lingkungan (indoor vs outdoor)
  • Tambahkan atraktan lain (asam laktat, octenol) untuk meningkatkan efektivitas
  • Kembangkan aplikasi mobile untuk monitoring dan pencatatan data
  • Integrasikan dengan program 3M Plus dan jumantik sekolah
  • Lakukan kerjasama dengan Puskesmas untuk validasi efektivitas di lapangan

"Sains bukan hanya tentang mengetahui, tapi tentang bertindak untuk kebaikan."